[Math] 행렬 기초

 

행렬

 

우선 기본적인 행렬에 대해서 적어보고자 한다.

 

MxN 행렬

 

우선 행렬이란 A11 ... Amn로 이루어진 성분의 집합 정도로 알고 가면 편하다.

• 여기서 M=N인 행렬을 정방행렬,
• 원소의 값이 모두 0인 행렬을 영행렬,
• 대각선 값(주대각 성분)이 모두 1이며 나머지 성분이 모두 0인 행렬을 단위행렬(I),
• 기존 행렬 Aij와 같은 원소를 Aji와 같이 성분의 위치를 변경시킨 것을 전치행렬(AT)이라고 하며, 전치행렬과 기존 행렬이 동일할 경우 이를 대칭행렬 이라고 한다.

 

또 행렬의 곱에 대해서

• 스칼라 곱은 기존 원소의 값에 스칼라 값을 곱해준다.
• 행렬끼리의 곱은 [M x N] x [N x O] 과 같이 첫번째 행렬의 열과, 두번째 행렬의 행 개수가 일치해야 한다.
• 행렬끼리의 곱은 특수한 경우를 제외하곤, 일반적으로 교환법칙이 성립하지 않는다.

 

행렬의 곱

 

 

---

 

 

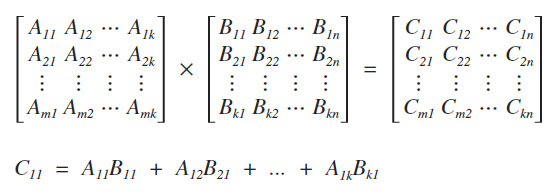
역행렬

 

역행렬이란 행렬 곱에서의 역원을 말하며, 행렬과 역행렬 곱의 결과는 단위행렬 (I)가 나오게 된다.

이 경우 행렬 A, A의 역행렬 B가 존재한다고 했을 때, AB = BA = I로 교환법칙이 성립한다.

 

또 다음과 같은 역행렬의 성질이 존재한다.

 

하지만 행렬의 역행렬이 항상 존재하는 것은 아니다.

역행렬이 존재하기 위해선 행렬식(Det)이 0이 아니어야만 하며, 정방행렬 이어야만 존재하고

역행렬이 존재하지 않는 행렬을 특이행렬, 역행렬이 존재하는 행렬은 가역행렬 또는 반특이행렬 이라고 한다.

 

우선 2x2 행렬의 역행렬을 구하는 방법은 비교적 간편하다.

 

 

다음은 3x3 행렬의 역행렬을 구하는 방법이다.

 

 

이 이상의 차원을 지닌 행렬의 경우엔 재귀함수와 같이 낮은 차원의 소인수를 계속해서 만들어가며 구해내면 된다.