평균
평균의 종류는 크게 세가지가 있다.
- 산술평균 (Mean) : 원소의 값을 모두 더한 다음, 원소의 수만큼 나눈 것
- 중앙값 (Median) : 원소를 정렬한 후 가운데에 있는 수. 갯수가 짝수일 경우 가운데 두개를 더한 뒤 2로 나눔.
- 최빈값 (Mode) : 원소의 값에 따른 갯수를 센 다음 가장 많은 수를 지닌 값.
극단치
추세선과 비교하여 눈에 띄게 동떨어진 데이터.
극단치를 다루는 방법은 세가지가 있다.
- 무시하기.
- 제거하기.
- 조정하기.
극단치의 의미 등을 고려하여 세가지 옵션 중 가장 적절한 것으로 사용하여 처리하는 것이 좋다.
왜도
실수 값 확률 변수의 확률 분포 비대칭성을 나타내는 지표.
왜도의 값은 음수가 될 수 있으며 정의되지 않을 수도 있다.
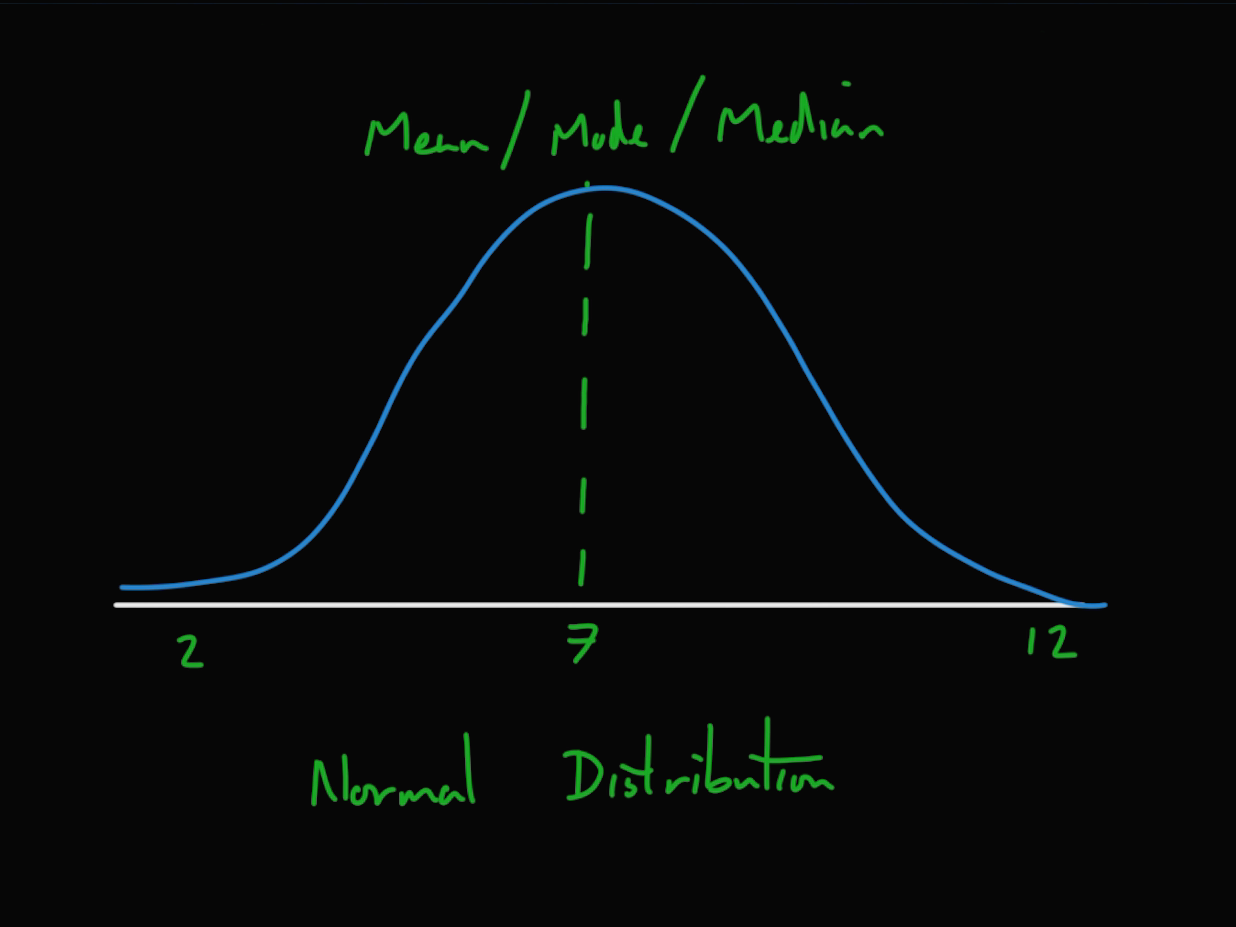
평균과 중앙값이 같으면 왜도는 0이 된다.
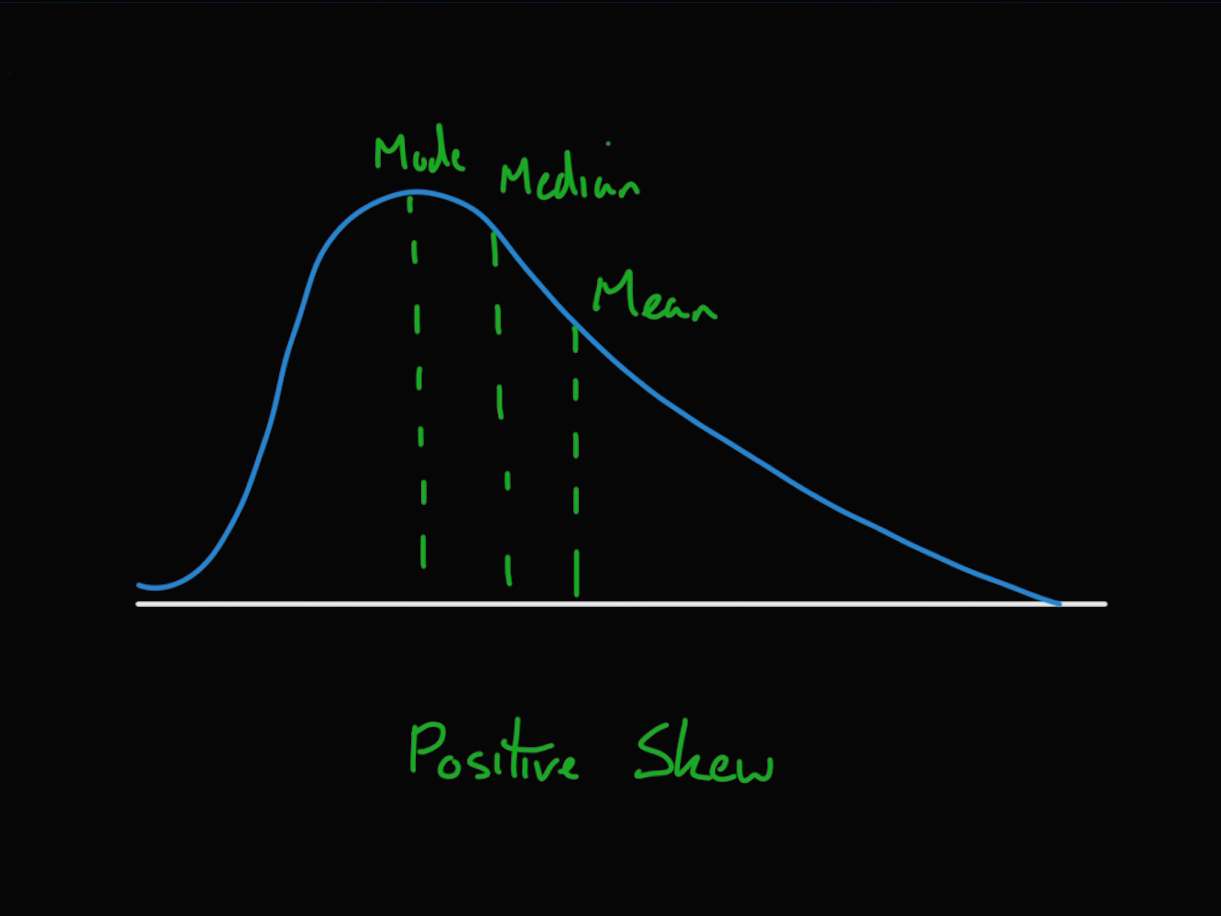
왜도가 양수일 때는 확률밀도함수의 오른쪽 부분에 긴 꼬리를 가지며 오른쪽으로 왜곡 되었다고 말한다.
자료가 왼쪽에 더 많이 분포해 있다는 것을 나타내며 산술평균과 중앙값은 항상 최빈값의 오른쪽에 위치한다.
왜도가 음수일 경우 확률밀도함수의 왼쪽 부분에 긴 꼬리를 가지며 왼쪽으로 왜곡 되었다고 말한다.
자료가 오른쪽에 더 많이 분포해 있다는 것을 나타내며 산술평균과 중앙값은 항상 최빈값의 왼쪽에 위치한다

사분위간 범위
자료를 같은 갯수로 4개로 나눈 각각의 값을 사분위수(quartile)라고 한다.
n개의 값이 있다면 중앙값이 2사분위수인 Q2이며, (Q2 + 1)/2 번째가 1사분위수인 Q1이고, (Q2 + n)/2 번째가 3사분위수인 Q3이다.
예를 들면
[ 1 2 3 3 4 4 4 5 7 10 ] 이라는 열개의 수가 존재할 때,
Q2는 중앙값인 4가 되며, Q1은 25% 지점인 3, Q3는 75% 지점인 5가 되며
사분위간 범위인 IQR = Q3 - Q1이므로 2가 되고, 범위인 Range는 Max - Min 이므로 10 - 1로 9가 된다.
분산과 표준편차
우선 분산과 표준편차에 대해서 알아보기 전에, 편차에 대해서 알아보자.
편차는 관측값이 평균으로부터 얼마나 떨어져 있는가를 나타내며
편차 = (관측값 - 평균)이고, 양수일수도 음수일수도 있다.
다음은 분산으로, 편차의 합을 제곱하고, 요소의 수로 나눈 것을 얘기하며
정확한 식은 아래와 같다.

표준편차는 분산의 제곱근을 말하며
제곱을 통해 다소 왜곡된 값인 분산을 제곱근 함으로써 왜곡을 크게 줄여준 값이다.
식은 아래와 같다.

표본집단의 경우 N-1로 나눠주는 이유는, 작은 수를 나눔으로써 표준편차의 값이 살짝 커지게 되고
살짞 커진 값이 표본집단에서 고려하지 못한 데이터에 대한 여유분이 되어준다.
이렇게 표준편차를 크게 만들고, 오차범위를 크게 만들어 표본에서 잃어버렸을 수 있는 데이터를 고려해 준다.
상관 ( r-value )
데이터 간에 관계가 있는지를 알려주는 개념.
데이터가 한 변수가 증가할 수록 다른 변수도 증가하는 오른쪽 위로 가는 방향의 관계 = 양의 상관관계라고 말하고
r-value = 양수이며, 값이 높을수록 상관관계가 높다는 것을 의미한다.
오른쪽 아래로 가는 방향의 관계 = 음의 상관관계 라고 하고 r-value = 음수이며, 값이 낮을수록 상관관계가 높다는 것을 의미한다.
마지막으로 전혀 상관이 없음을 나타내는 r-value = 0이다.
r-value를 구하는 방식은 다음과 같다.
- 각각 x,y축에 대한 산술평균 구하기.
- 각 축의 요소에 대한 편차 구하기.
- 공분산 (두 축의 요소에 대한 편차를 곱한 뒤 평균을 구함) 구하기
- 공분산을 각 축의 표준편차의 곱으로 나눔.
결론적으로 r = cov(x,y) / (σx * σy) 라는 식이 나온다.
정규화
데이터 분석을 수행하면서 많이 겪는 문제중 하나가 데이터 단위의 불일치이다.
이를 해결하는 방법으로 Normalization(정규화)가 있다.
이 방법은 대표적으로 2개 이상의 대상이 단위가 다를 때 대상 데이터를 같은 기준으로 볼 수 있게 해준다.
즉, 다른 데이터와 같이 분석을 할 때에도 표준화 또는 정규화된 데이터를 이용하면 단위 차이 문제 등에서 벗어나서 쉽게 사용할 수 있다.
정규화의 공식은 다음과 같다.

아래쪽의 식은 0~1 사이가 아닌 a~b의 숫자로 나타내고 싶을 때 활용이 가능한 식이다.
확률밀도함수와 누적분포함수
확률밀도함수 (PDF) : 연속 확률 변수를 나타내는 함수. 확률 질량 함수의 연속형 버전.
누적분포함수 (CDF) : 주어진 확률 변수가 특정 값보다 작거나 같은 확률을 나타내는 함수 '누적'이라는 이름은 특정 값보다 작은 값들의 확률을 모두 누적해서 구한다는 의미에서 붙여진 이름이다.

역누적분포함수는 누적분포함수의 역함수를 말하며
누적분포함수
X : 확률변수
Y : 누적 확률
역누적분포함수
X : 누적확률
Y : 확률변수
로 변환된다.
'Math & Physicss' 카테고리의 다른 글
| [Math] 좌표계 변환 행렬 (0) | 2022.02.02 |
|---|---|
| [Math] Scale, Rotation, Translation 변환 행렬 (SRT 변환) (0) | 2022.02.01 |
| [Math] 선형보간과 이징함수 (0) | 2022.01.25 |
| [Math] 행렬 기초 (0) | 2022.01.24 |
| [Math] 벡터의 반사와 평면사영 (0) | 2022.01.24 |